Exercice 2.8

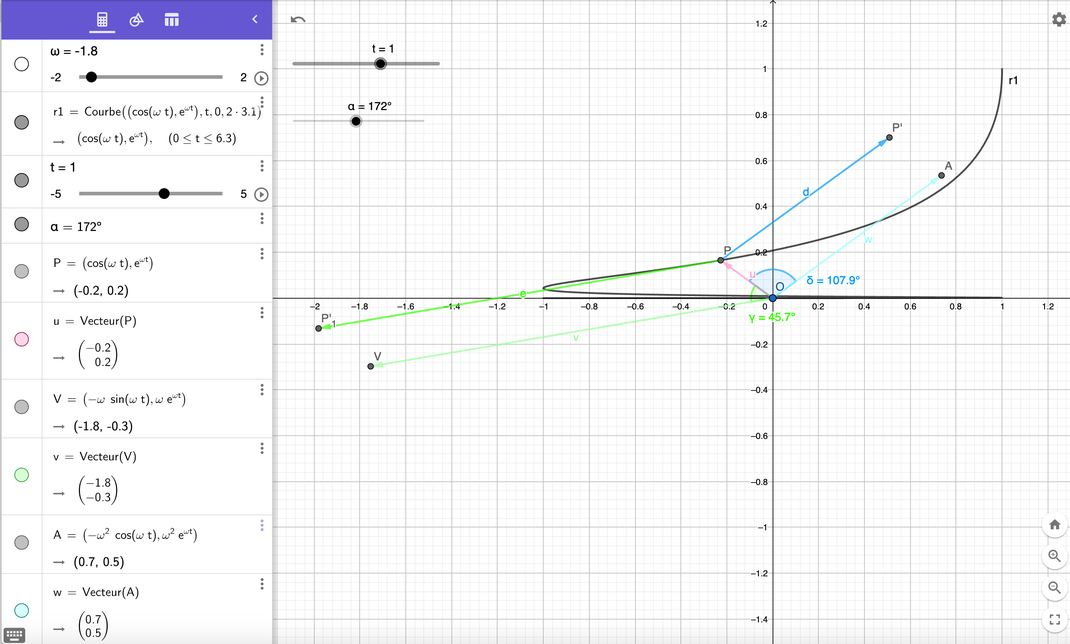
1) ` vec r = (cos omega t, e^(omega t) ) = (r_x (t), r_y (t)) `
` vec v = dot vec r = (frac (dr_x (t))(dt), frac(dr_y (t))(dt) ) = ( v_x(t), v_y(t) ) `
` = (-omega sin omega t, omega e^(omega t) )`
` vec a = dot vec v = (frac (dv_x (t))(dt), frac(dv_y (t))(dt) ) = ( a_x(t), a_y(t) ) `
` = (-omega^2 cos omega t, omega^2 e^(omega t) )`
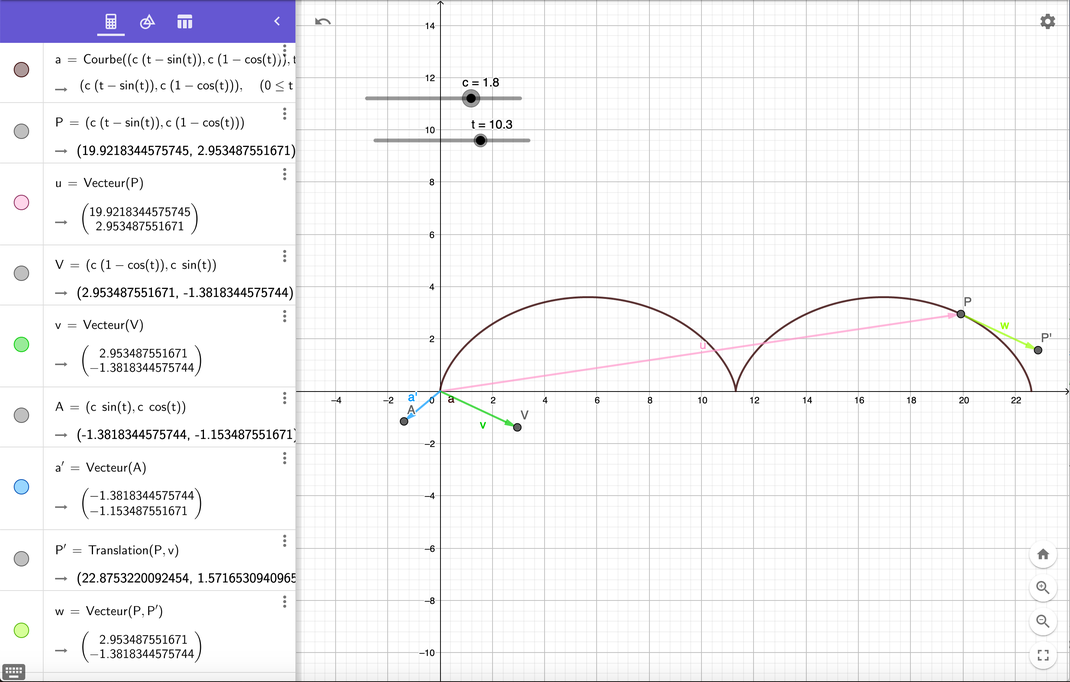
Les représentations graphiques des différents vecteurs ont été effectuées à l'aide de Geogebra 'Calculatrice Graphique' en ligne :
J'ai laissé intentionnellement la partie programmation (si l'on peut dire) des différentes courbes.
Plus d'informations sur l'utilisation de Geogebra sont données dans le complément 2.2 .
Dans cette partie gauche de programmation, on reconnait, de haut en bas les différentes déclarations :
- la courbe avec le curseur 'omega' qu'il a fallu impérativement utiliser pour obtenir une courbe intéressante,
- le point P que l'on fait circuler sur la courbe à l'aide du curseur 't',
- le vecteur position 'u',
- le vecteur vélocité 'v', associé au point V obtenu par dérivation du vecteur position,
- le vecteur accélération 'w', associé au point A obtenu par dérivation du vecteur vélocité.
Ce sont les graphes demandés.
En plus :
- les angles entre les vecteurs (u, v) et (u, w) qui permettent de vérifier que les vecteurs 'u' et 'v' ne sont pas orthogonaux systématiquement,
- le vecteur P P'1 parallèle (colinéaire) à 'v' , mais issu de P, qui visualise que 'v' en P est bien tangent à la courbe.
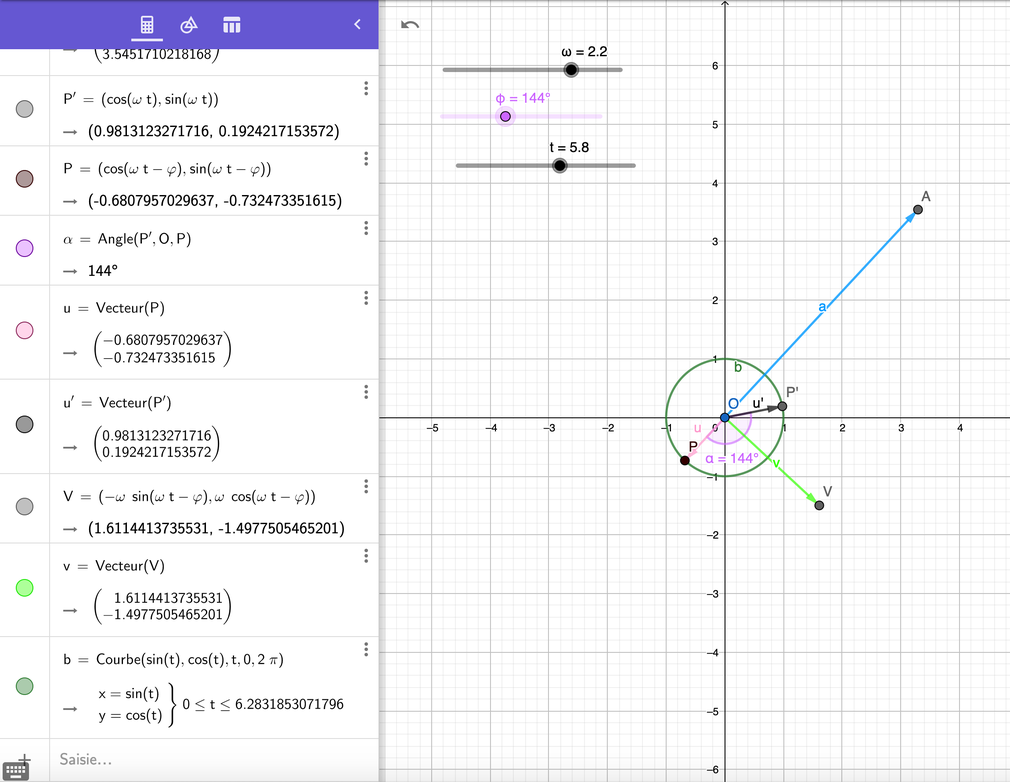
2) ` vec r = (cos(omega t - phi), sin (omega t - phi)) `
` vec v = dot vec r = (-omega sin (omega t - phi), omega cos(omega t - phi)\ )` en utilisant la dérivée de fonction de fonction vue à l'exercice 2.4 .
` vec a = dot vec v = (-omega^2 cos (omega t - phi), -omega^2 sin(omega t - phi)\ )` là aussi.
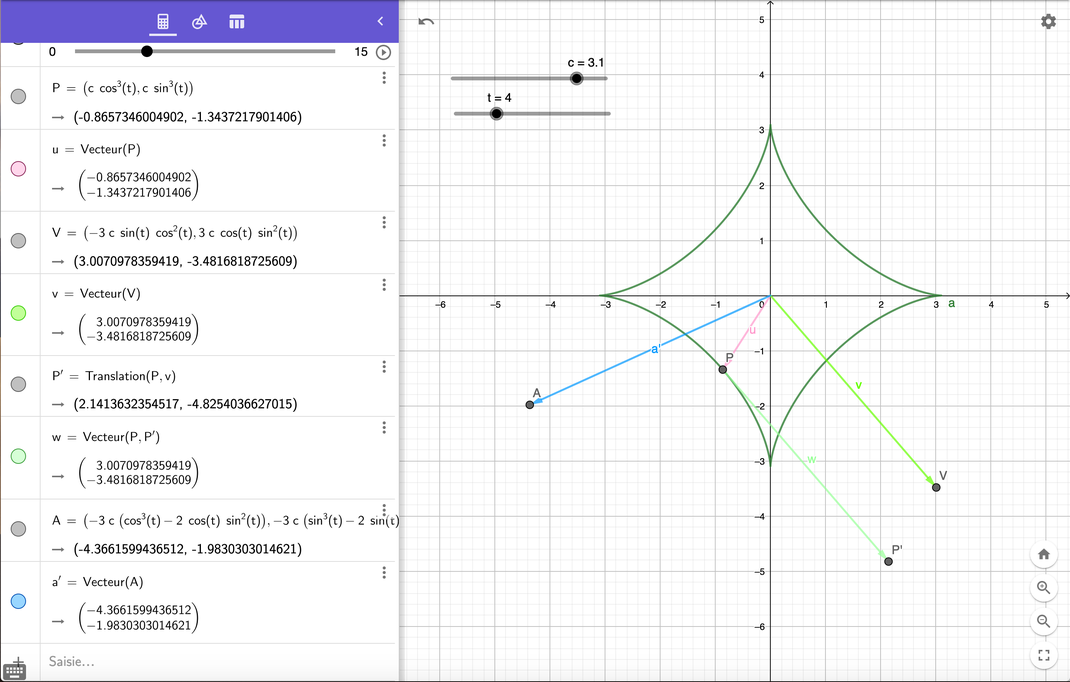
3) ` vec r = (c cos^3(t), c sin^3(t) ) `
` vec v = (-3c sin t cos^2t, 3c cos t sin^2 t) `
` vec a = (-3c (cos^3t - 2 cos t sin^2 t), -3c (sin^3t - 2 sin t cos^2 t) `
4) ` vec r = ( c (t - sin t), c (1 - cos t) ) `
` vec v = ( c (1 - cost), c sint) `
` vec a = ( c sin t), c cos t) `