1) Énergie cinétique.

Restons en coordonnées cartésiennes pour commencer :

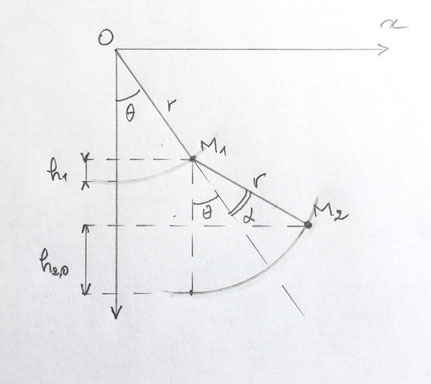
        ` x_1 = r\ sin theta ` 
        ` y_1 = r\ cos theta ` 

        ` x_2 = x_1 + r\ sin(theta + alpha) `  
        ` y_2 = y_1 + r\ cos(theta + alpha) `          avec la figure adéquate ci-dessus pour rester avec les expressions utilisées.

        ` x_2 = r\ (sin theta + sin(theta + alpha)) ` 
        ` y_2 = r\ (cos theta + cos(theta + alpha)) `  

L'énergie cinétique est donnée par :

        ` T = frac(1)(2)m v^2 ` 

avec :
        ` v^2 = sum_i dot q_i^2  `               pour prendre la notation avec les coordonnées généralisées


        ` T_1 = frac(1)(2)m v_1^2 ` 
             ` = frac(1)(2)m (dot x_1^2 + dot y_1^2) ` 

avec :
        `dot x_1 = r\ dot theta cos theta `                     puisque   ` r = "Cte" `  et    ` theta = theta(t) ` 
        `dot y_1 = - r\ dot theta sin theta ` 

et :
        `dot x_1^2 = r^2\ dot theta^2 cos^2 theta ` 
        `dot y_1^2 = r^2\ dot theta^2 sin^2 theta ` 

ce qui nous donne pour ` T_1 ` :

        ` color(brown) (T_1) = frac(1)(2)m \ r^2 dot theta^2 (cos^2 theta + sin^2 theta ) ` 

             `color(brown) ( = frac(1)(2)m \ r^2 dot theta^2 )`                  en étant maintenant en coordonnées polaires


        


En partant de :
        ` x_2 = r\ (sin theta + sin(theta + alpha)) ` 
        ` y_2 = r\ (cos theta + cos(theta + alpha)) `  

on obtient d'abord :
        ` dot x_2 = r(dot theta cos theta + (dot theta + dot alpha) cos (theta + alpha) ) ` 
        ` dot y_2 = - r(dot theta sin theta + (dot theta + dot alpha) sin (theta + alpha) ) ` 

        ` dot x_2^2 = r^2(dot theta^2 cos^2 theta + (dot theta + dot alpha)^2 cos^2 (theta + alpha) + 2 dot theta (dot theta + dot alpha) cos theta cos (theta + alpha) ) ` 
        ` dot y_2^2 = r^2(dot theta^2 sin^2 theta + (dot theta + dot alpha)^2 sin^2 (theta + alpha) + 2 dot theta (dot theta + dot alpha) sin theta sin (theta + alpha) ) ` 

d'où :
        ` dot x_2^2 + dot y_2^2 = r^2 (dot theta^2(sin^2 theta + cos^2 theta) + (dot theta + dot alpha)^2 (cos^2(theta + alpha) + sin^2(theta + alpha) ) ` 
                                ` + 2 dot theta(dot theta + dot alpha)(cos theta cos(theta + alpha) + sin theta sin(theta + alpha) ) ` 



        ` cos a cos b + sin a sin b = cos(a-b) `             pour la dernière formule entre parenthèses juste ci-dessus
        ` cos(-a) = cos a ` 



        ` dot x_2^2 + dot y_2^2 = r^2 ( dot theta^2 + (dot theta + dot alpha)^2 + 2 dot theta(dot theta + dot alpha) cos (theta - (theta + alpha)) )` 
                       ` = r^2 ( dot theta^2 + (dot theta + dot alpha)^2 + 2 dot theta(dot theta + dot alpha) cos alpha ) ` 
et :
        `color(brown) ( T_2 = frac(1)(2)m r^2 ( dot theta^2 + (dot theta + dot alpha)^2 + 2 dot theta(dot theta + dot alpha) cos alpha ) )` 



Ce qui donne pour l'énergie cinétique totale :

        ` T = T_1 + T_2 ` 

           ` = frac(1)(2)m r^2 ( dot theta^2 ) + frac(1)(2)m r^2 ( dot theta^2 + (dot theta + dot alpha)^2 + 2 dot theta(dot theta + dot alpha) cos alpha ) ` 

        `color(blue) ( T = m r^2 ( dot theta^2 + frac((dot theta + dot alpha)^2)(2) + dot theta(dot theta + dot alpha) cos alpha ) )`                 qui est bien l'énergie cinétique utilisée.

2) Énergie potentielle.



    ` h_1 = r - r cos theta ` 
        `\ = r(1 - cos theta) ` 




    ` h_2 = h1 + h_(2,0) ` 

    ` h_(2,0) = R - r cos (theta + alpha) ` 
            ` = r(1 - cos (theta + alpha)) ` 

    ` h_2 = r(1 - cos theta) + r(1 - cos (theta + alpha)) `
        ` = r(2 - cos theta - cos (theta + alpha)) ` 



Et donc pour l'énergie potentielle totale :

        ` V = V_1 + V_2 ` 
            ` = mgh_1 + mgh_2 ` 
            ` = mgr ( (1 - cos theta) + (2 - cos theta - cos (theta + alpha)) `

        `color(purple) ( V(theta, alpha) = mgr(3 - 2 cos theta - cos (theta + alpha)) )` 


Ces évaluations de   ` h_1 `  et   ` h_2 `  correspondent au dénivelé restant à parcourir par les masses.
Elles ne sont cependant valables que si le système de référence a comme Origine le point bas du 
mouvement du pendule comme on le fait habituellement.

Mais ce n'est pas le cas ici puisque l'Origine est située au point de rotation du pendule, donc à son point haut.
Et c'est la notion  ` color(blue)("d'Altitude") `   qui doit être prise en compte comme expliqué dans le Complément 7.2 .



Les altitudes vont donc être respectivement pour le pendule double :

        ` - r cos theta `                         pour la masse   ` m `  au point   ` M_1 `  ,
        ` - r cos theta - r cos(theta + alpha) `         pour la masse   ` m `  au point   ` M_2 ` 

et l'énergie potentielle va donc s'écrire :

        ` V = -mg\ r cos theta - mg(r cos theta + r cos(theta + alpha) ) ` 
            ` = - 2mg \ r cos theta - mg\ r cos(theta + alpha) ` 
soit :
        ` color(blue)(V = -\ g (2 cos theta + cos(theta + alpha) )`             pour   ` m = 1,\ r = 1 ` 

ce qui est bien l'expression attendue (avec   ` theta + alpha `  au lieu de   ` theta - alpha `  pour être en cohérence avec 
le développement page 156 et le schéma en haut de page qui en découle).


Le Lagrangien utilisé dans l'exercice 6 sera donc :

        ` L = T - V ` 

        `color(blue) ( L = m r^2 ( dot theta^2 + frac((dot theta + dot alpha)^2)(2) + dot theta(dot theta + dot alpha) cos alpha ) + mgr(2 cos theta + cos (theta + alpha) ) )`