Nous avons déjà déterminé l'équation du mouvement en coordonnées polaires dans l'Exercice 6.5
mais là c'est en coordonnées cartésiennes ` x(t),\ y(t) ` que l'équation est demandée.
L'énergie cinétique est :
` T = frac(1)(2)m(dot x^2 + dot y^2) `
et l'énergie potentielle :
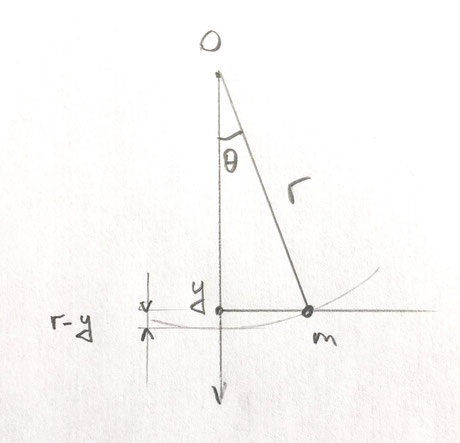
` V = mgh = mg (r - y) ` ` (1) ` comme l'indique le schéma ci-dessus,
ou :
` V = mg(r - sqrt(r^2 - x^2) )` ` (2) ` si l'on utilise la relation ` x^2 + y^2 = r^2 `
Le démarrage avec un angle ` theta ` se retrouvant dans les conditions initiales :
` x(t=0) = x_0 = r sin theta `
` y(t=0) = y_0 = r cos theta ` l'angle ` theta ` étant ici une constante et pas une variable.
1) Potentiel ` (1) ` .
Le Lagrangien est alors :
` L = frac(1)(2)m(dot x^2 + dot y^2) - mg (r - y) `
En appliquant les équations d'Euler-Lagrange pour trouver l'équation du mouvement, on obtient :
` frac(del L)(del dot x) = m dot x\ \ \ => \ \ \ frac(d)(dt) frac(del L)(del dot x) = m ddot x `
` frac(del L)(del x) = 0 `
et :
` frac(del L)(del dot y) = m dot y\ \ \ => \ \ \ frac(d)(dt) frac(del L)(del dot y) = m ddot y `
` frac(del L)(del y) = mg `
soit le système d'équations linéaires :
`color(brown) ( { ( m ddot x = 0 ), ( m ddot y = mg ) :} )`
avec les conditions initiales :
` x_0 = r sin theta `
` y_0 = r cos theta `
Lorsque l'on résoud ce système, on obtient :
` m ddot x = 0 `
` dot x = c_1 `
` x = c_1t + c_0 = v_x(0)t + x_0 `
` x = v_x(0)t + r\ sin theta `
de même :
` y = frac(1)(2)g""t^2 + v_y(0)t + r\ cos theta `
et avec :
` v_x(0) = v_y(0) = 0 ` si on ne fait que lâcher le pendule,
cela donne :
`color(brown) ( { ( x = r\ sin theta ), ( y = frac(1)(2)g\ t^2 + r\ cos theta ) :} )`
ce qui n'est certainement pas exact .
2) Potentiel ` (2) ` .
Si on utilise la formulation ` (2) ` du potentiel, le Lagrangien devient :
` L = frac(1)(2)m(dot x^2 + dot y^2) - mg (r - sqrt(r^2 - x^2)) `
et les équations d'Euler-Lagrange :
` frac(del L)(del dot x) = m dot x => frac(d)(dt) frac(del L)(del dot x) = m ddot x `
` frac(del L)(del x) = - mg ( - frac(-2x)( 2 sqrt(r^2 - x^2) ) )`
` = - frac(mgx)(sqrt(r^2 - x^2) )`
et :
` frac(del L)(del dot y) = m dot y => frac(d)(dt) frac(del L)(del dot y) = m ddot y `
` frac(del L)(del y) = 0 `
ce qui donne le système d'équations :
` color(brown) ( { ( m ddot x = class{cmjx-lg} {- frac(mgx)(sqrt(r^2 - x^2) ) } ), ( m ddot y = 0 ) :} )`
avec les mêmes conditions initiales que précédemment :
` x_0 = r\ sin theta `
` y_0 = r\ cos theta `
` v_x(0) = v_y(0) = 0 `
Le système est un peu plus consistant mais certainement pas exact non plus, vu l'équation avec ` ddot y \ ` semblable à celle rencontrée avec le Potentiel.
Des REMARQUES seraient les bienvenues. Merci d'avance.
Quels sont les éléments qui font que les équations d'Euler-Lagrange ne nous donnent pas de réponse satisfaisante ?
3) Méthode de la Conservation de l'Energie .
Avec les équations en coordonnées polaires utilisées dans l'Exercice 6.5 :
` T = frac(1)(2) m r^2 dot theta^2 `
` V = mgr (1 - cos theta) `
l'équation de la Conservation de l'Energie nous conduisait au résultat, à savoir :
` frac(dT)(dt) + frac(dV)(dt) = 0 `
et :
` frac(dT)(dt) = mr^2 dot theta \ ddot theta `
` frac(dV)(dt) = mgr \ dot theta\ sin theta `
donc :
` mr^2 dot theta \ ddot theta + mgr \ dot theta\ sin theta = 0 `
` r\ ddot theta + g\ sin theta = 0 ` en simplifiant par ` mr^2 dot theta `
`color(brown) ( ddot theta = - frac(g)(r) sin theta )` l'équation recherchée du mouvement.
Cela nous donne en coordonnées cartésiennes :
` T = frac(1)(2)m(dot x^2 + dot y^2)`
` V = mg (r - y) `
` frac(dT)(dt) = m (dot x ddot x + dot y ddot y) `
` frac(dV)(dt) = - mg \ dot y `
et donc :
` m (dot x ddot x + dot y ddot y) - mg \ dot y = 0 `
`color(brown) ( dot x ddot x + dot y (ddot y - g) = 0 (1) )`
avec les conditions :
` x^2 + y^2 = r^2 `
` 2 x dot x + 2 y dot y = 0 ` en ayant dérivé.
`color(brown) ( x dot x + y dot y = 0 (2) )`
L'ensemble de ces deux expressions est la réponse la plus cohérente que je puisse donner pour le moment.