Déroulement :

        1)   équations du mouvement 

        2)  coordonnés polaires 

        3)  éclaircissements sur le symbole ` nabla ` 

        4)  continuons

        5)  simplifications et obtention de la solution

        6)  tracé des courbes

        7)  énergie totale

De la même manière que pour l'exercice 5.2, nous allons y aller doucement car la correction L5e3 du MAST ne m'apparait pas des plus
facile.
Mais on va arriver à une solution.

1) Commencons comme précédemment par calculer les équations qui permettent de déterminer le mouvement :

On a le potentiel 'V' qui est maintenant :
        ` V = frac(k)(2(x^2 + y^2)) `

avec les forces suivant les différents axes données par :
        ` F_i({x}) = - frac( del V({x}) )(del x_i) `

et donc :



`\ frac(d)(dt) (frac(u)(v)) = frac (u^'v - v^'u)(v^2) `   ou   `\ frac(d)(dt) (frac(1)(v)) = frac ( - v^')(v^2) `   lorsque `\ u = 1`



        ` frac(del V)(del x) = - frac(4x\ k)( 4(x^2 + y^2)^2 ) = - frac(kx)( (x^2 + y^2)^2 ) `

        ` frac(del V)(del y) = - frac(4y\ k)( 4(x^2 + y^2)^2 ) = - frac(ky)( (x^2 + y^2)^2 ) `

ce qui nous donne ensuite :

        ` m ddot x = frac(kx)( (x^2 + y^2)^2 ) `

        ` ddot x = frac(k)(m) frac(x)( (x^2 + y^2)^2 ) = frac(omega^2x)( (x^2 + y^2)^2 )`  en posant `\ omega = sqrt frac(k)(m) `  comme lors de l'exercice précédent.

        ` ddot y = frac(omega^2y)( (x^2 + y^2)^2 )`

Mais le problème est que nous n'avons identifié aucune solution à ce type d'équation qui est, rappelons le, une équation différentielle. 
Ce n'est plus le type ` \ \ ddot x = -omega^2x`  et nous ne savons pas le résoudre.

2) Comme c'est le terme ` x^2 + y^2 `  qui nous gêne, nous allons utiliser les Coordonnées polaires pour le mettre sous la
forme ` x^2 + y^2 = rho^2 `  , `\ 'rho '`   devenant notre nouvelle variable en posant `\ x = rho cos theta, \ y = rho sin theta`  .

Ces Coordonnées polaires sont présentées dans le Complément 5.2 , les coordonnées précédentes étant
des coordonnées 'cartésiennes' puisqu'elles suivent les Ox et Oy.

Le potentiel 'V' va maintenant s'écrire :
        ` V = frac(k)(2 rho^2) `  ou `\ \ V = frac(k)(2 r^2) `  si l'on a choisi     `\x^2 + y^2 = r^2 `    comme dans le corrigé du MAST.

et sa dérivée partielle :
        ` color(brown) ( frac(del V)(del rho) = - frac(k)(2) frac(2 rho)(rho^4) = - frac(k)(rho^3) )`  en ayant appliqué la règle de dérivation d'un quotient énoncée quelques lignes au-dessus.

Avant d'aller plus loin, revenons à la méthode que nous avions utilisée lors de l'exercice précédent pour déterminer 
nos équations du mouvement.

On avait d'abord écrit :
        ` F_x = - frac(del V)(del x) = - k\ x `

        ` F_y = - frac(del V)(del y) = - k\ y `     pour la relation avec le Potentiel.

et puis :
        ` F_x = m ddot x `
        ` F_y = m ddot y `     pour la relation avec la 2ème loi de Newton.

qui sont des relations 'scalaires', c'est-à-dire non vectorielles.
Mais, et c'est important, les relations 'vectorielles' sous-entendues s'appuyaient sur les axes cartésiens. Elles étaient les suivantes :

        ` vec F = m vec a = m(a_i vec i + a_j vec j) = m(ddot x vec i + ddot y vec j) `
        ` vec F = color(brown) (-(frac(del V)(del x) vec i + frac(del V)(del y) vec j) ) = - ( kx\ vec i + ky\ vec j) `

et on avait égalé les composants de chaque vecteur suivant la règle "lorsque deux vecteurs sont égaux leurs composantes sont égales" :

        ` m ddot x = -kx`   pour le vecteur de base ` 'vec i' `
        ` m ddot y = -ky`   pour le vecteur de base ` 'vec j' `


Comme nous venons de changer de système de coordonnées et donc de 'vecteurs de base', nous allons réécrire les relations précédentes
en fonction de ces nouveaux vecteurs, à savoir `\ vec u_rho \ "et"\ vec u_theta ` .

3) Avant de continuer plus loin, nous allons préciser une écriture qui a déjà été utilisée dans le corrigé L5e2 du MAST pour l'exercice 5.2.

Il s'agit du symbole `\ grad`   ('nabla' ou 'del') qui reprend une formule que nous avons utilisée quelques lignes au-dessus, 
à savoir  `color(brown) ( frac(del V)(del x) vec i + frac(del V)(del y) vec j )`  et que nous appellerons donc maintenant aussi `\ vec grad V `   'grad V' .

Et comme nous avions utilisé `\ vec grad V `   (sans le savoir) avec les coordonnées 'cartésiennes', il nous faut la même chose maintenant en 'coordonnées
polaires' pour continuer à utiliser la formule `\ x^2 + y^2 = rho^2 `   qui nous simplifie la vie.

Les explications sont données dans le Complément 5.3 et la formule s'écrit :

        ` vec grad V(rho cos theta, rho sin theta) = frac(del V)(del rho) vec u_rho + frac(1)(rho) frac(del V)(del theta) vec u_theta `

En écrivant `\ vec grad V(rho cos theta, rho sin theta)`   car nous avons dit que `\ x = rho\ cos theta\ "et"\ y = rho\ sin theta `   .

Rassurez-vous, cela a l'air compliqué, mais c'est pour la bonne cause, et la simplification va arriver immédiatement.

4) Continuons.
Notre potentiel `\ V = frac(k)(2 rho^2) `   ne dépend en effet que de `\ 'rho' `   et donc la dérivée partielle `\ frac(del V)(del theta) = 0 ` .

Donc pour la partie Potentiel , on a :
        ` vec F = - vec grad V = - (frac(del V)(del rho) vec u_rho + \ 0 xx vec u_theta) `  ,

et comme nous avions déjà calculée  `color(brown) ( \ frac(del V)(del rho) )`   précédemment, nous avons maintenant sous la forme vectorielle :
        ` vec F = - frac(del V)(del rho) vec u_rho = -( -frac(k)(rho^3) vec u_rho ) = frac(k)(rho^3) vec u_rho `       (1)


        OUF ! Comme dit Leonard Susskind dans le volume 2, ne sortez pas la planche de surf tout de suite, 
        nous avons dépassé une grosse difficulté !

Maintenant, pour la partie Force,   `\ m vec a `   va devoir s'exprimer sous la forme :
        ` vec F = m vec a = m(a_theta vec u_theta + a_rho vec u_rho) `

Les termes `\ a_theta \ "et"\ a_rho`   ont été calculés dans le Complément 5.2 et l'équation devient :
        ` m vec a = m((rho ddot theta + 2 dot rho dot theta) vec u_theta + (ddot rho - rho dot theta^2) vec u_rho) `    (2)


Le début du corrigé de cet exercice par le MAST consiste justement à présenter les coordonnées polaires et l'expression
des deux vecteurs `\ vec v`   et `\ vec a`  dans ces coordonnées. La comparaison des deux approches est toujours intéressante.



et donc comme les relations (1) et (2) sont égales :
        ` m((rho ddot theta + 2 dot rho dot theta) vec u_theta + (ddot rho - rho dot theta^2) vec u_rho) = frac(k)(rho^3) vec u_rho `

Ce qui donne en identifiant les composantes de chaque vecteur comme pour la méthode précédente :
        ` color(brown) ( rho ddot theta + 2 dot rho dot theta = 0 )`            (a)
        ` color(brown) ( m(ddot rho - rho dot theta^2) = frac(k)(rho^3) )`   (b)

sans oublier que `\ x = rho(t)\ cos theta(t)\ "et"\ y = rho(t)\ sin theta(t) `


C'est le système d'équations différentielles qui va nous permettre de trouver les équations recherchées du mouvement.
Heureusement avec des simplifications, sinon on ne saurait pas les résoudre non plus !

5) Maintenant les simplifications.

Regardons comment apparaissent les simplifications pour ` rho(t) `  et  ` theta(t) ` .

1) Si le mouvement est circulaire, son équation s'écrit ' ` color(brown) (\ rho = R = "Constante" )` '   en coordonnées polaires.
et donc ses dérivées sont nulles :   ` dot rho = ddot rho = 0 `

2) L'équation (b) devient pour  ` theta(t) ` :
        ` 0 - mR dot theta^2 = frac(k)(R^3) `
        ` color(brown) ( dot theta^2 = -frac(k)(m\ R^4) ) `

Comme le membre de gauche de l'équation est un carré, l'égalité n'a de sens que si `\ k < 0 ` .
ce qui donne :
        ` dot theta(t) = +- sqrt frac(-k)(m) frac(1)(R^2) = + sqrt frac(-k)(m) frac(1)(R^2)`   en ne prenant que le cas positif pour `\ dot theta(t) `  .

        `color(brown) ( theta(t) = sqrt frac(-k)(m) frac(1)(R^2)t + c_1 ) `    et si `\ theta(0) = 0\ => \ c_1 = 0 `    (S1) 





Considérons maintenant l'équation (a) :
        ` color(brown) ( rho ddot theta + 2 dot rho dot theta = 0 ) `    avec `\ rho = R, \ dot rho = 0 `
        ` R ddot theta(t) = 0 `
        ` ddot theta(t) = 0 `    ` => `    ` dot theta(t) = c_2 `
et donc :
        ` color(brown) (theta(t) = c_2 t + c_3 )`               (S2) 

Les solutions  (S1) et (S2)  sont compatibles pour  ` theta(t) `  puisqu'elles sont de la même forme.


Et nous pouvons donc dire que nous avons trouvé une solution en 'coordonnées polaires' pour un mouvement circulaire :

        ` color(blue)( { (rho ,= R ), (theta(t) ,= frac(omega)(R^2)t ) :} )` 

avec  ` omega = sqrt frac(-k)(m) `         ` k < 0 ` 

En reprenant les relations `\ x = rho(t)\ cos theta(t)\ "et"\ y = rho(t)\ sin theta(t) `  pour revenir en 'coordonnées cartésiennes', on obtient :

        `color(blue) ( { ( x = R cos frac(omega)(R^2)t ), ( y = R sin frac(omega)(R^2)t ) :} )` 



Les courbes circulaires n'ont pas toute la même période puisque la vitesse de rotation dépend du rayon 'R'. 
Plus le rayon R est grand, plus la période est longue puisque la vitesse angulaire `\ Omega = frac(omega)(R^2) `   est plus petite.





La solution en ligne L5e3 du MAST indique que l'équation (a) `\ rho ddot theta + 2 dot rho dot theta = 0 `  conduit à la 
relation     `frac(d)(dt) rho^2 dot theta = 0 `      après une petite manipulation, c'est-à-dire `\ rho^2 dot theta = "Constante" ` .

Cela correspond à la conservation du moment angulaire (ou cinétique) de la particule, ce qui est une propriété importante.
Plus exactement quand on l'écrit `\ m rho^2 dot theta = "Constante" ` , cela exprime que la danseuse en patin à glaces tourne plus vite 
lorsqu'elle ramène ses bras le long du corps. 

Son moment cinétique  `\ m rho^2 `   diminue et donc sa vitesse de rotation `\ dot theta `  augmente.



6) Tracé des courbes.
On peut maintenant représenter la solution par les courbes suivantes :

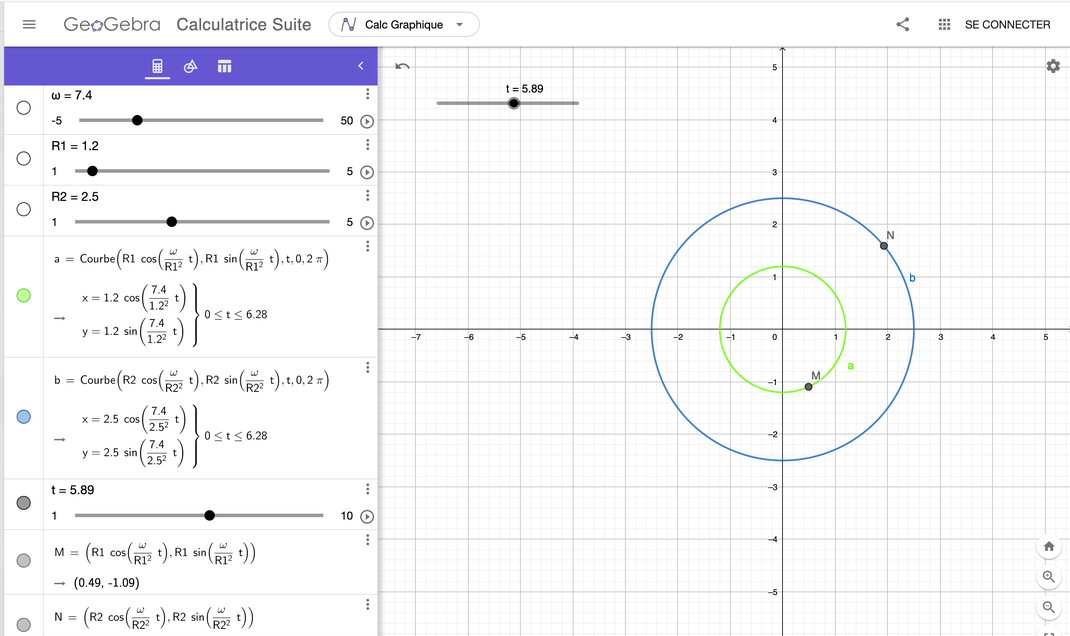
Le mode vidéo sur le 'Curseur t' permet de bien visualiser la différence de vitesse de rotation des différentes courbes circulaires.

7) Energie totale :

De même manière qu'à l'exercice précédent on reprend la formule (8) page 112 :
        ` frac(dT)(dt) + frac (dV)(dt) = 0 `     qu'il faut vérifier.

avec :
        ` frac(dT)(dt) = sum_i m_i dot x_i ddot x_i  `

        ` - frac(dV)(dt) = - sum_i dot x_i frac(del V)(del x_i)  `     ` del V\ "ou"\ del V(x_1, x_2, . . . ,x_n)` ou `\ del V({x}) `


Cette dernière expression ci-dessus est plus amplement expliquée dans le Complément 5.1 .



Dans notre cas nous avons les équations du mouvement :

        ` x_1(t) = R cos frac(omega)(R^2) t `

        ` x_2(t) = R sin frac(omega)(R^2) t` 


avec les dérivées successives :

        ` dot x_1 =   -R frac(omega)(R^2) sin frac(omega)(R^2) t = - frac(omega)(R) sin frac(omega)(R^2) t`
        ` dot x_2 = R frac(omega)(R^2) cos frac(omega)(R^2) t = frac(omega)(R) cos frac(omega)(R^2) t ` 

        ` ddot x_1 = - frac(omega)(R) frac(omega)(R^2) cos frac(omega)(R^2) t = - frac(omega^2)(R^3) cos frac(omega)(R^2) t `

        ` ddot x_2 = - frac(omega)(R) frac(omega)(R^2) sin frac(omega)(R^2) t = - frac(omega^2)(R^3) sin frac(omega)(R^2) t ` 


Pour ` frac(dT)(dt) `  avec  ` m_1 = m_2 = m `  , on arrive à :

        ` frac(dT)(dt) = m\ [ dot x_1\ ddot x_1 + dot x_2\ ddot x_2 ] ` 

        ` color(blue) (frac(dT)(dt) ) = m\ [ (- frac(omega)(R) sin frac(omega)(R^2) t) (- frac(omega^2)(R^3) cos frac(omega)(R^2) t ) + (frac(omega)(R) cos frac(omega)(R^2) t) (- frac(omega^2)(R^3) sin frac(omega)(R^2) t ) ] `

                ` = m frac(omega^3) ( R^4)\ ( sin frac(omega)(R^2) t \ cos frac(omega)(R^2) t - cos frac(omega)(R^2) t \ sin frac(omega)(R^2) t) `
                ` color(blue) (= 0 ) `


et pour ` frac(dV)(dt) `  avec   ` V = frac(k)(x_1^2 + x_2^2) ` 

        ` frac(del V)(del x_1) = - frac(2kx_1)( (x_1^2 + x_2^2)^2 ) ` 

                  ` = - frac(2kx_1)( R^4 )`

        ` frac(del V)(del x_2) = - frac(2kx_2)( (x_1^2 + x_2^2)^2 ) ` 

                  ` = - frac(2kx_2)( R^4 )`



        ` color(blue) ( frac(dV)(dt) ) = dot x_1\ frac(del V)(del x_1) + dot x_2\ frac(del V)(del x_2) ` 

                ` =  (- frac(omega)(R) sin frac(omega)(R^2) t) ( frac(- 2kx_1 )(R^4) ) + (frac(omega)(R) cos frac(omega)(R^2) t)( frac(- 2kx_2 )(R^4) ) `

                ` = frac(2k omega)(R^5) ( color(brown) (x_1) sin frac(omega)(R^2)t - color(brown) (x_2) cos frac(omega)(R^2)t ) `
    
                ` = frac(2k omega)(R^5) (color(brown) (R cos frac(omega)(R^2)t ) \ sin frac(omega)(R^2)t - color(brown) (R sin frac(omega)(R^2)t )\ cos frac(omega)(R^2)t ) `        en ayant remplacé ` x_1 ` et ` x_2 `  par leur valeur.

                ` color(blue) ( = 0 ) `

donc :
        `color(blue) ( frac(dV)(dt) + frac(dT)(dt) = 0 )`    ce que l'on devait vérifier pour pouvoir dire que l'énergie totale du système est conservée.


Les énergies potentielle et cinétique sont séparément conservées.
Nous ne sommes plus dans le cas classique de l'exercice 5.2 précédent où l'énergie potentielle se transformait en énergie 
cinétique et réciproquement.

Quel est le sens de cette observation ? J'ai un doute sur ce résultat.
Des compléments seraient intéressants sur la relation entre la forme du potentiel V en ` frac(k)(r^2),\  frac(k)(r), \ kr ` 
et la conservation associée de l'énergie.

Je n'arrive pas aux mêmes résultats que le corrigé du MAST.

Des commentaires et des remarques seront donc les bienvenus.

La conclusion du corrigé du MAST est qu'il n'y a aucune orbite circulaire stable.

Cela ne veut pas dire qu'il n'y a pas de mouvement circulaire possible.

D'autant que la stabilité est un sujet délicat à étudier à ce niveau du livre.

Pour rappel, l'exercice n° 1 de ce chapitre demande de prouver que `\ frac (dv^2)(dt) = 2 v dot v ` !

L'instabilité est abordée à partir de 'l'énergie potentielle effective' qui est traitée dans l'annexe en fin d'ouvrage. Nous essaierons d'y voir plus clair à ce moment.