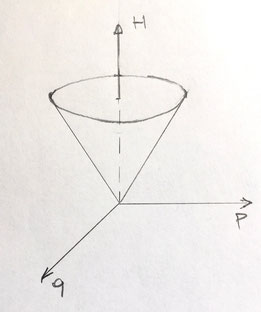
L'Hamiltonien obtenu étant :

        ` H = frac{omega}{2} (p^2 + q^2) ` 

l'image donnée par cette équation est la surface d'un cône comme indiqué ci-dessus.

A chaque valeur de ` H ` correspond une trajectoire circulaire d'équation :

        ` p^2 + q^2 = R^2 `        avec         ` R = sqrt( frac{2H}{omega} ) `  

Et les vitesses respectives de chaque composante de l'espace des phases sont données par les équations :

        ` dot p = - omega q `             ` (1) ` 
        ` dot q = omega p `                   ` (2) ` 

Comme à chaque valeur de ` H ` correspond une trajectoire circulaire nous pouvons passer en coordonnées polaires :

        ` p = R cos theta(t)    =>    dot p = -R\ dot theta sin theta(t) ` 
        ` q = R sin theta(t)    =>    dot q = R\ dot theta cos theta(t) ` 

ce qui donne respectivement dans les équations ` (1)\ \  "et" \ \ (2) ` :

        ` -R\ dot theta sin theta(t) = - omega R sin theta(t) ` 

et après simplification :
        ` dot theta = omega ` ,

       ` R\ dot theta cos theta(t) = omega R cos theta(t) ` 

et après simplification :
        ` dot theta = omega ` 

On obtient bien donc    ` color(blue) (dot theta = omega )`        quel que soit ` R ` et donc quel que soit ` H ` ,

ce qui signifie que la vitesse de rotation du point dans l'espace des phases est la même pour toutes les orbites,
ce que l'on voulait démontrer.