1) Equations du mouvement.

Remarque :

Comme la correction proposée par le MAST, l5e2.pdf est un peu ardue, nous allons y aller plus doucement.

- - - - - - - -

a) Les forces dérivent du potentiel :

` F_i = - frac(del V)(del x_i) `

Comme il y a deux dimensions (les axes Ox et Oy), les forces s'écrivent :

` F_x = -frac(del V)(del x) = -frac(1)(2) k\ 2x = - kx `

` F_y = -frac(del V)(del y) = -frac(1)(2) k\ 2y = - ky `    qui est l'équation habituelle d'une force exercée par un ressort suite à un allongement de y (ou x).

b) Le mouvement d'une masse 'm' est donné par la 2ème loi de Newton :

` m_i ddot x_i = F_i({x}) `

ce qui donne ici avec ` m_1 = m_2 = m`

` m \ ddot x = F_x = -kx `

` m \ ddot y = F_y = -ky `

ou en écrivant sous la forme vue page 80 :

` ddot x = - frac (k)(m) x = - omega^2 x `   avec `\ omega = sqrt frac (k)(m) `

` ddot y = - frac (k)(m) y = - omega^2 y `

La solution de ce type d'équation différentielle a été vérifiée dans l'exercice 3.4, et les deux solutions vont s'écrire respectivement :

` color (blue) (x(t) = A cos omega t + B sin omega t )`   et ce sont les équations du mouvement que l'on recherchait.

` color(blue) ( y(t) = C cos omega t + D sin omega t )`

On peut l'écrire aussi sous forme d'un vecteur position, comme étudié et représenté lors de l'exercice 8 du chapitre 2 :

` color(blue) ( vec r (A cos omega t + B sin omega t, C cos omega t + D sin omega t) )`

2) Les orbites circulaires :

Leur présence ou non va dépendre des paramètres A, B, C et D.

Comme vu précédemment, le mouvement d'une particule dépend de sa position initiale et de sa vitesse initiale.

Avec deux dimensions, ces caractéristiques sont `\ x(0), y(0), v_x(0), v_y(0) ` :

` x(0) = A cos(0) + B sin(0) = A xx 1 + B xx 0 = A ` ,   ` x(0) `  représente ici l'élongation du ressort quand on le lache.

` v_x = -A omega sin omega t + B omega cos omega t `

` v_x(0) = -A omega sin (0) + B omega cos (0) = B omega ` ,    et `\ v_x(0) `  sa vitesse initiale éventuelle.

` y(0) = C cos(0) + D sin(0) = C xx 1 + D xx 0 = C `

` v_y = -C omega sin omega t + D omega cos omega t `

` v_y(0) = -C omega sin (0) + D omega cos (0) = D omega `

Prenons par exemple le cas `\ A = C = 2 `   et ` \ B = D = 0 `  qui donne l'équation du mouvement :

` x(t) = 2 cos omega t `

` y(t) = 2 cos omega t `

On obtient la courbe :

en ayant créé (voir le Complément 2.2) la courbe 'a' et le point 'M' comme indiqué, ainsi que le curseur 't' de valeurs entre `\ 0 ` et `\ 2 pi` .

Ce n'est pas un cercle mais une droite ` y = x ` (en revenant à une équation non paramétrée) avec `\ x ` qui varie entre 0 et 2 .

De plus le mouvement animé permet de voir le point M se mouvoir sur cette portoin de droite si on clique sur le symbole 'vidéo' de l'élément 'curseur t'dans la colonne de gauche.

Il peut y avoir des orbites circulaires si la courbe de mouvement est un cercle, donc de forme :

` color(blue) ( x(t) = kappa cos omega t )`

` color(blue) (y(t) = kappa sin omega t )`

Voir aussi la Remarque 2 du Complément 10.2 .

puisque si on élève ces deux expressions au carré, et qu'on les additionne, on obtient :

` x^2 + y^2 = kappa^2 (cos^2 omega t + sin^2 omega t) = kappa^2 = R^2 `     qui est l'équation d'un cercle de rayon R =`\ kappa`

et donc avec les valeurs respectives de paramètres :

` color(blue) ( A = kappa = x(0) )`     comme élongation initiale sur l'axe Ox

` color(blue) ( B = 0 )`       pas de vitesse initiale le long de l'axe Ox

` color(blue) ( C = 0 )`       pas d'élongation initiale sur l'axe Oy

` color(blue) ( D = kappa )`       qui permet de déterminer vitesse initiale le long de l'axe Oy

On a en effet vu quelques lignes avant que :

` color(blue) (v_y(0) = D omega) `

Comme ` D = kappa = x(0)   =>   color(blue) (v_y(0) = omega \ x(0) )`

ce qui donne comme courbes avec `omega = 1 ` :

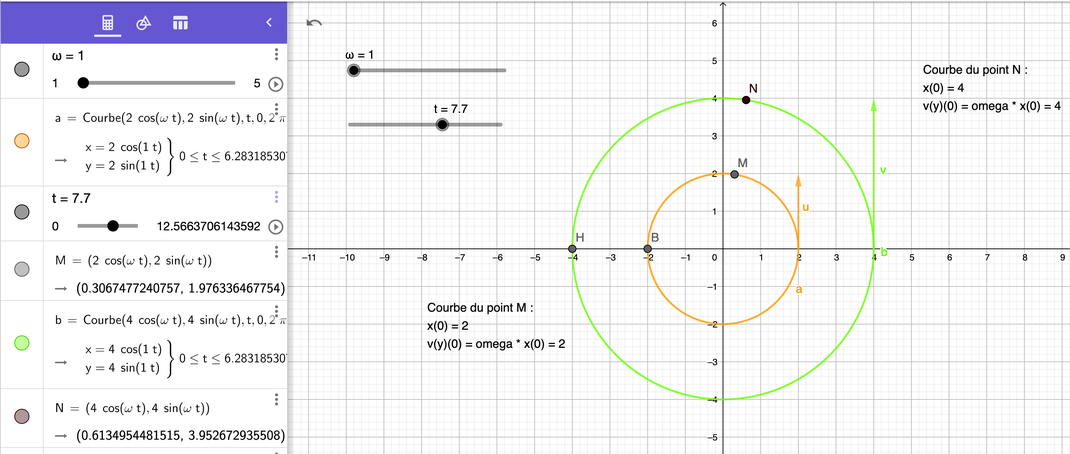
Toutes les courbes circulaires étant en ` ( cos omega t, sin omega t) ` , la durée d'une rotation est donnée par `\ omega T = 2 pi\ "et"\ omega` étant la vitesse angulaire,

donc `\ T = frac(2 pi)(omega) = 6,28\ "secondes puisque"\ omega = 1\ "radian par seconde"` dans les courbes ci-dessus (avec le mode vidéo toujours disponible).

3) Energie totale :

On va donc reprendre la formule (8) page 112 :

` frac(dT)(dt) + frac (dV)(dt) = 0 `     qu'il faut vérifier.

avec :

` sum_i m_i dot x_i ddot x_i = frac(dT)(dt) `

` - sum_i dot x_i frac(del V)(del x_i) = - frac(dV)(dt) `     ` del V\ "ou"\ del V(x_1, x_2, . . . ,x_n)` ou `\ del V({x}) `

Cette dernière expression est plus amplement expliquée dans le Complément 5.1 .

Dans notre cas nous avons :

` x_1(t) = A cos omega t + B sin omega t `   qui sont les équations du mouvement.

` x_2(t) = C cos omega t + D sin omega t `

` dot x_1 = -A omega sin omega t + B omega cos omega t `

` dot x_2 = -C omega sin omega t + D omega cos omega t `

` ddot x_1 = -A omega^2 cos omega t - B omega^2 sin omega t = - omega^2 x_1(t) `  

` ddot x_2 = -C omega^2 cos omega t - D omega^2 sin omega t = - omega^2 x_2(t)`

Avec ` m_1 = m_2 = m `

on arrive à :

` frac(dT)(dt) = m\ [ (-A omega sin omega t + B omega cos omega t) (- omega^2 x_1(t) ) `

` + (-C omega sin omega t + D omega cos omega t) (- omega^2 x_2(t) ) ] `

et :

` frac(dV)(dt) = (-A omega sin omega t + B omega cos omega t)(k\ x) `

` + (-C omega sin omega t + D omega cos omega t)(k\ y) `

En se souvenant que `\ omega = sqrt frac (k)(m)  => \ k = m omega^2 \ \ "et" \ x = x_1(t), \ y = x_2(t) `

et en mettant `\ m `  en facteur, on obtient :

` frac(dV)(dt) = m [(-A omega sin omega t + B omega cos omega t)(omega^2 x_1(t)) `

` + (-C omega sin omega t + D omega cos omega t)(omega^2 x_2(t)) ]`

` = - frac(dT)(dt) `

donc :

`color(blue) ( frac(dV)(dt) + frac(dT)(dt) = 0 )`    ce que l'on devait vérifier pour pouvoir dire que l'énergie totale du système est conservée.