Tout d'abord, ce complément est dû à la remarque préalable de Mathieu Bivert, et aux échanges qui ont suivi.
Donc, merci à lui.
Nous prendrons un pendule simple pour plus de facilité.
Cette notion d'Altitude est utilisée par Léonard Susskind page 157, ainsi que dans d'autres articles sur internet, pour le calcul de
l'énergie potentielle.
Et cette utilisation ne donne pas les mêmes résultats qu'avec le dénivelé restant parcouru par une masse.
L'énergie potentielle que l'on exprime naturellement dans un premier
temps s'appuie sur le référentiel ` y'O'x' ` et l'on obtient :
` V = mg\ h `
` = mg\ y_1^' ` avec ` h = y_1^' = r - r cos theta `
` V = mg(r - r cos theta) `
Le calcul du potentiel s'appuie sur le dénivelé restant.
Mais la figure 3 page 155 s'appuie sur une origine en ` O ` , c'est à dire le référentiel ` xOy ` .
Il va donc y avoir un changement de coordonnées.
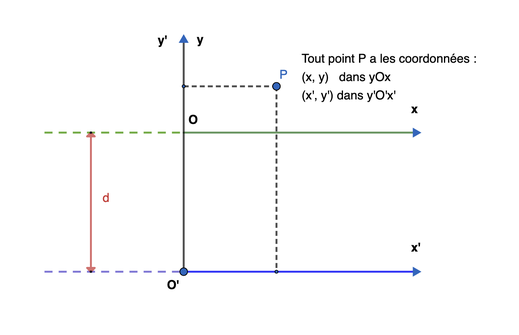
Tout point ` P ` a les coordonnées ` (x,\ y) ` dans le repère ` xOy `
et ` (x^',\ y^') ` dans le repère ` x^'O^'y^' ` .
avec :
` x^' = x ` et ` x = x^' `
` y^' = y + d ` ` y = y^' - d `
et dans notre cas ` d = r ` .
Dans le référentiel ` x'O'y' ` , l'énergie potentielle s'écrivait :
` V = mg\ y_1^' `
et maintenant dans le référentiel ` xOy ` :
` V = mg\ y_1 ` avec ` y_1 = y_1^' - r `
` = mg(y_1^' - r) `
` = mg((r - r cos theta) - r) `
` = - mgr cos theta `
et l'on retrouve bien la formule utilisée page 157 pour le pendule double, ainsi que dans la littérature, comme par exemple l'article sur
le Pendule Double dans Wikipedia.
Pour le calcul de l'énergie potentielle, ` color(blue)("l'Altitude") ` est donc l'équivalent du dénivelé restant lorsqu'on prend l'origine du mouvement
du pendule à son axe de rotation (en haut), au lieu de le prendre à son lieu d'arrivée (en bas).